Month: February 2014

A new week, a new assignment. This week I get to optimize a piece of code that renders a “glass” ball on a background, letting through some of the color hidden in the background image. Puzzling on my own and talking to classmates helped in creating code which I couldn’t get any faster. I’ve learned a lot doing this and discussing it with peers.

The initial code draws a colorful landscape with a black & white overdraw on it, making it a greyscale and darker image. The ball samples pixels from the colorful version of the image. The goal of this week’s assignment is to optimize using several rules of thumb, “Get rid of expensive operations”, “Precalculate”, “Use the power of 2”, “Avoid conditional jumps”, and “Get out early”. High-level optimizations were not specifically required, but makes the code a lot faster. I will show both versions of “Game.cpp”, mine and the unoptimized one.

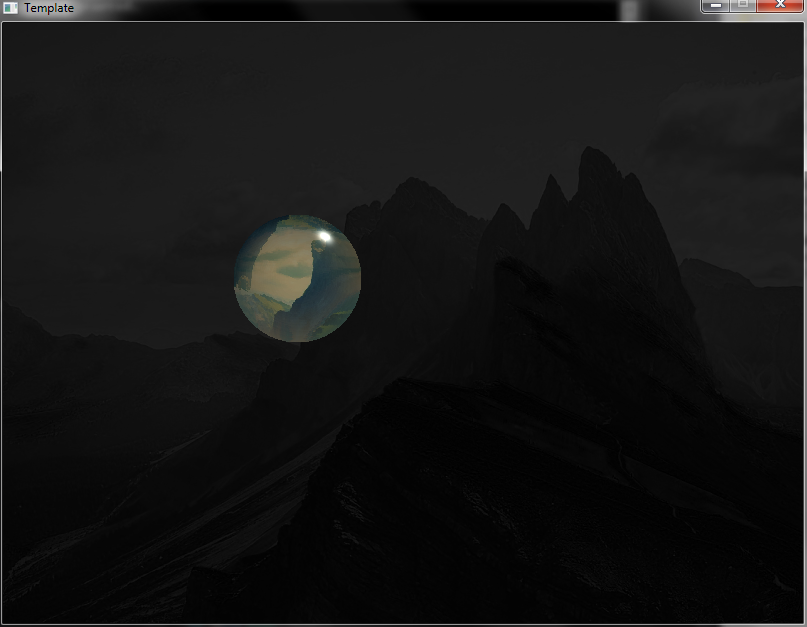
This is how the glass-ball effect looks.

The initial code was written by my teacher, Jacco Bikker, for the NHTV, and is intended to be optimized. The most relevant bit is in the “Game.cpp” and is as follows.
[code language=”cpp”]#include "game.h"
#include "surface.h"

using namespace Tmpl8;

// ———————————————————–
// Scale a color (range: 0..128, where 128 is 100%)
// ———————————————————–
inline unsigned int ScaleColor( unsigned int orig, char scale )
{
const Pixel rb = ((scale * (orig & ((255 << 16) + 255))) >> 7) & ((255 << 16) + 255);
const Pixel g = ((scale * (orig & (255 << 8))) >> 7) & (255 << 8);
return (Pixel)rb + g;
}

// ———————————————————–
// Draw a glass ball using fake reflection & refraction
// ———————————————————–
void Game::DrawBall( int bx, int by )
{
Pixel* dst = m_Surface->GetBuffer() + bx + by * m_Surface->GetPitch();
Pixel* src = m_Image->GetBuffer();
for ( int x = 0; x < 128; x++ )
{
for ( int y = 0; y < 128; y++ )
{
float dx = (float)(x – 64);
float dy = (float)(y – 64);
int dist = (int)sqrt( dx * dx + dy * dy );
if (dist < 64)
{
int xoffs = (int)((dist / 2 + 10) * sin( (float)(x – 50) / 40.0 ) );
int yoffs = (int)((dist / 2 + 10) * sin( (float)(y – 50) / 40.0 ) );
int u1 = (((bx + x) – 4 * xoffs) + SCRWIDTH) % SCRWIDTH;
int v1 = (((by + y) – 4 * yoffs) + SCRHEIGHT) % SCRHEIGHT;
int u2 = (((bx + x) + 2 * xoffs) + SCRWIDTH) % SCRWIDTH;
int v2 = (((by + y) + 2 * yoffs) + SCRHEIGHT) % SCRHEIGHT;
Pixel refl = src[u1 + v1 * m_Image->GetPitch()];
Pixel refr = src[u2 + v2 * m_Image->GetPitch()];
int reflscale = (int)(63.0f – 0.015f * (1 – dist) * (1 – dist));
int refrscale = (int)(0.015f * (1 – dist) * (1 – dist));
dst[x + y * m_Surface->GetPitch()] =
ScaleColor( refl, 41 – (int)(reflscale * 0.5f) ) + ScaleColor( refr, 63 – refrscale );
float3 L = Normalize( float3( 60, -90, 85 ) );
float3 p = float3( (x – 64) / 64.0f, (y – 64) / 64.0f, 0 );
p.z = sqrt( 1.0f – (p.x * p.x + p.y * p.y) );
float d = min( 1, max( 0, Dot( L, p ) ) );
d = powf( d, 140 );
Pixel highlight = ((int)(d * 255.0f) << 16) + ((int)(d * 255.0f) << 8) + (int)(d * 255.0f);
dst[x + y * m_Surface->GetPitch()] = AddBlend( dst[x + y * m_Surface->GetPitch()], highlight );
}
}
}
}

// ———————————————————–
// Initialize the game
// ———————————————————–
void Game::Init()
{
m_Image = new Surface( "testdata/mountains.png" );
m_BallX = 100;
m_BallY = 100;
m_VX = 1.6f;
m_VY = 0;
}

// ———————————————————–
// Draw the backdrop and make it a bit darker
// ———————————————————–
void Game::DrawBackdrop()
{
m_Image->CopyTo( m_Surface, 0, 0 );
Pixel* src = m_Surface->GetBuffer();
unsigned int count = m_Surface->GetPitch() * m_Surface->GetHeight();
for ( unsigned int i = 0; i < count; i++ )
{
src[i] = ScaleColor( src[i], 20 );
int grey = src[i] & 255;
src[i] = grey + (grey << 8) + (grey << 16);
}
}

// ———————————————————–
// Main game tick function
// ———————————————————–
void Game::Tick( float a_DT )
{
m_Surface->Clear( 0 );
DrawBackdrop();
DrawBall( (int)m_BallX, (int)m_BallY );
m_BallY += m_VY;
m_BallX += m_VX;
m_VY += 0.2f;
if (m_BallY > (SCRHEIGHT – 128))
{
m_BallY = SCRHEIGHT – 128;
m_VY = -0.96f * m_VY;
}
if (m_BallX > (SCRWIDTH – 138))
{
m_BallX = SCRWIDTH – 138;
m_VX = -m_VX;
}
if (m_BallX < 10)
{
m_BallX = 10;
m_VX = -m_VX;
}
}[/code]

I will not dive in too much depth on what the pieces of the code does, but Init runs once, Tick runs every frame, DrawBackdrop draws the dark and grey overlay on top of the bright coloured landscape, which is visible through the ball drawn with DrawBall. The things to optimize will be drawing the background (with currently DrawBackdrop) and DrawBall. I did not pay attention to memory usage, as that isn’t the intention of the excersize. This is the code that I ended up with:
[code language=”cpp”]#include "game.h"
#include "surface.h"
#include <iostream>
#include <time.h>

using namespace Tmpl8;

Surface* imageWithBackdrop;

// ———————————————————–
// Scale a color (range: 0..128, where 128 is 100%)
// ———————————————————–
inline unsigned int ScaleColor( unsigned int orig, int scale )
{
const Pixel rb = ((scale * (orig & ((255 << 16) | 0xFF))) >> 7) & ((255 << 16) + 255);
const Pixel g = ((scale * (orig & (255 << 8))) >> 7) & (255 << 8);
return (Pixel)rb + g;
}

// ———————————————————–
// Draw a glass ball using fake reflection & refraction
// ———————————————————–
const float3 L = Normalize(float3(60, -90, 85));
unsigned int imageWidth;
unsigned int imageHeight;
int distances[128 * 128];
Pixel highlights[128 * 128];
int xOffs[128 * 128];
int yOffs[128 * 128];
int reflScales[128 * 128];
int refrScales[128 * 128];
const static int pitch = SCRWIDTH;

#define BALLS 100

struct Ball
{
float m_X, m_Y, m_VX, m_VY;
};
Ball balls[BALLS];

void Game::DrawBall( int bx, int by )
{
static Pixel* src = m_Image->GetBuffer();
Pixel* dst = m_Surface->GetBuffer() + bx + by * m_Surface->GetPitch();

for (int y = 0; y < 128; ++y )
{
for ( int x = 0; x < 128; ++x )
{
unsigned int index = (y << 7) + x;

if (distances[index] < 64)
{
unsigned int u1 = ((((bx + x) – (xOffs[index] << 1)) + imageWidth) << 22) >> 22;
unsigned int v1 = ((((by + y) – (yOffs[index] << 1)) + imageHeight) << 22) >> 12;
unsigned int u2 = (((bx + x) + xOffs[index] + imageWidth) << 22) >> 22;
unsigned int v2 = (((by + y) + yOffs[index] + imageHeight) << 22) >> 12;

Pixel refl = src[u1 + v1]; //Reflection
Pixel refr = src[u2 + v2]; //Refraction

dst[x + y * pitch] =
AddBlend(
ScaleColor(refl, reflScales[index]) + ScaleColor(refr, refrScales[index]),
highlights[index]
);
}
}
}
}

// ———————————————————–
// Draw the backdrop and make it a bit darker
// ———————————————————–
void Game::DrawBackdrop()
{
m_Image->CopyTo(m_Surface, 0, 0);
Pixel* src = m_Surface->GetBuffer();
unsigned int count = m_Surface->GetPitch() * m_Surface->GetHeight();
for (unsigned int i = 0; i < count; i++)
{
src[i] = ScaleColor(src[i], 20);
int grey = src[i] & 255;
src[i] = grey + (grey << 8) + (grey << 16);
}
}

void DrawBackground(Surface* a_Target)
{
memcpy(a_Target->GetBuffer(), imageWithBackdrop->GetBuffer(),
imageWithBackdrop->GetPitch() * imageWithBackdrop->GetHeight() * sizeof(Pixel));
}

// ———————————————————–
// Initialize the game
// ———————————————————–
#define TEST_ITERATIONS 512
void Game::Init()
{
srand((unsigned int)time(0));
m_Image = new Surface("testdata/mountains.png");
imageWidth = m_Image->GetWidth();
imageHeight = m_Image->GetHeight();

for (int y = 0; y < 128; y++)
{
float dy = (float)(y – 64);
for (int x = 0; x < 128; x++)
{
float dx = (float)(x – 64);
int dist = (int)sqrt(dx * dx + dy * dy);
distances[y * 128 + x] = dist;
}
}

for(int y = 0; y < 128; y++)
{
int dy = y – 64;
float pY = dy / 64.0f;

for (int x = 0; x < 128; x++)
{
xOffs[y * 128 + x] = (int)(((distances[y * 128 + x] >> 1) + 10) * sin((x – 50) / 40.0f));
xOffs[y * 128 + x] <<= 1;
yOffs[y * 128 + x] = (int)(((distances[y * 128 + x] >> 1) + 10) * sin((y – 50) / 40.0f));
yOffs[y * 128 + x] <<= 1;

reflScales[y * 128 + x] = (int)(63.0f – 0.015f * (1 – distances[y * 128 + x]) * (1 – distances[y * 128 + x]));
reflScales[y * 128 + x] = 41 – (reflScales[y * 128 + x] >> 1);
refrScales[y * 128 + x] = (int)(0.015f * (1 – distances[y * 128 + x]) * (1 – distances[y * 128 + x]));
refrScales[y * 128 + x] = 63 – refrScales[y * 128 + x];

float3 p((x – 64) / 64.0f, pY, 0);
p.z = sqrt(1.0f – (p.x * p.x + p.y * p.y));

float d = Dot(L, p);
if (d > 0.96f) //Approximate value, anything below this doesn’t affect the highlight.
{
d = min(1, max(0, d));
d = pow(d, 140);
auto di = (int)(d * 255.0f);
Pixel highlight = (di << 16) + (di << 8) + di;

highlights[y * 128 + x] = highlight;
}
else
{
highlights[y * 128 + x] = 0;
}
}
}

for (int i = 0; i < BALLS; i++)
{
balls[i].m_X = (float)(80 + rand()%(SCRWIDTH-230));
balls[i].m_Y = (float)(16 + rand() % (SCRHEIGHT – 230));
balls[i].m_VX = 1.6f;
balls[i].m_VY = 0;
}

DrawBackdrop();
imageWithBackdrop = new Surface(m_Surface->GetPitch(), m_Surface->GetHeight());
memcpy(imageWithBackdrop->GetBuffer(), m_Surface->GetBuffer(),
m_Surface->GetPitch() * m_Surface->GetHeight() * sizeof(Pixel));

unsigned long long timings[TEST_ITERATIONS];
for (int iterations = 0; iterations < TEST_ITERATIONS; iterations++)
{
TimerRDTSC timer;
timer.Start();
DrawBall(300, 300);
timer.Stop();
timings[iterations] = timer.Interval();
}
unsigned long long total = 0;
for (int i = 0; i < TEST_ITERATIONS; i++)
{
total += timings[i];
}
total /= TEST_ITERATIONS;
std::cout << total << " is average for DrawBall\n";
TimerRDTSC timer;
timer.Start();
DrawBackground(m_Surface);
timer.Stop();
std::cout << timer.Interval() << std::endl;
}

// ———————————————————–
// Main game tick function
// ———————————————————–
void Game::Tick( float a_DT )
{
DrawBackground(m_Surface);

for (int i = 0; i < BALLS; i++)
{
DrawBall((int)balls[i].m_X, (int)balls[i].m_Y);
balls[i].m_X += balls[i].m_VX;
balls[i].m_Y += balls[i].m_VY;
balls[i].m_VY += 0.2f;
if (balls[i].m_Y >(SCRHEIGHT – 128))
{
balls[i].m_Y = SCRHEIGHT – 128;
balls[i].m_VY = -0.96f * balls[i].m_VY;
}
if (balls[i].m_X > (SCRWIDTH – 138))
{
balls[i].m_X = SCRWIDTH – 138;
balls[i].m_VX = -balls[i].m_VX;
}
if (balls[i].m_X < 10)
{
balls[i].m_X = 10;
balls[i].m_VX = -balls[i].m_VX;
}
}
}[/code]

Background

I started off with the background, which was rendering slow due to the DrawBackdrop every frame. The background image never changes, which means drawing the backdrop only once on a copy of the landscape and then drawing that pre-rendered surface as background would save me quite some cycles. I moved the call to DrawBackdrop to the Init-function and drew that to a new surface.

This saved me a lot of cycles. The cycles on itself don’t say a lot, but in comparison to optimized results, they do. Going from 100 to 10 cycles would be 10 times faster, while 100 itself doesn’t give any valuable information away. The rendering of the background with the backdrop costed me about 1871784 cycles on average (on 10 tests). The optimized DrawBackground, using the pre-rendered surface and memcpy, uses roughly 285000 cycles on average (on 512 tests). This is about 15.2% of the unoptimized version. Clearing the screen wasn’t necessary, so that line is removed in the final code.

The Ball

For the optimizations performed on drawing the ball, I will discuss the before mentioned topics. The original code uses 4912748 cycles on average for 512 tests. The optimized version uses about 433500 on average, with 512 tests. That means there’s only 8.8% left of the cost!

Get rid of expensive operations (and use the power of 2)

The original code uses a lot of expensive operations. Most of that stuff can be precalculated, which is what I went for. I did try some other ideas before I started to move those calculations to the Init function. Here’s a short list of things I’ve figured out, some with help of my classmates.

• Changing “powf” to “pow” gives an enormous reduction in cycles. This is because “pow” takes an integer as power and “powf” takes a float, which is a lot harder to calculate. Since the input is 140, it could just be an integer.
• Reducing the calls to “pow” increases performance a lot. “pow” is still quite expensive, so we’d want to reduce its use as much as we can. The code using “pow” draws a specular highlight on the ball, but that’s just a small dot. Doing “pow” for every pixel while only about 5% should need it is a waste. I approximated a number of about 0.96 (depending on the power), where every result of the Dot-product higher than that will draw a pixel for the specular highlight. 96% less calls to “pow” is great.
• The distance calculations were faster with floats. I didn’t expect this, since integer operations are practically always faster. But, I read somewhere that the compiler might use SIMD to optimize floating-point operations, making it a lot faster. This is why you should always test and record, instead of blindly changing code which you think might run faster.
• Modulo is slow. It can be used to have looping textures, but the operation is slow. The original code used modulo on the window width, but it sampled colours (for refraction and reflection) from the image provided with the project. The fortunate thing is that the background image has a dimension of 1024×640. Since 1024 is a power of 2, you can use a logical and operator (&) to scrape off the bits not included in the 1024-range, making it wrap neatly. This speeds up the code enormously, since it saves two modulo calls per pixel per ball. The height isn’t a power of two, but we can adjust the image to make it so. Using PhotoShop, I padded the height to 1024, repeating the image for sampling purposes. Now I can do the same thing with the height, removing all uses of modulo.
• Bitshifting is faster than logical and (&). In the previous list item, I removed the modulo calls, by replacing them with logical ands, greatly increasing speed. But, since we’re only using the first 10 bits, we can shift 22 bits to the left, truncating all those bits and then shifting them back to get the wrapped value between 0 and 1023. This saved several thousand cycles on average.
• int-float conversions are slow. “(int)(reflscale * 0.5f)” converts “reflscale” to a float to do the multiplication and then converts that back to an int. Since 0.5 is a reciprocal of a power of 2, we can just use a bitshift to divide the number by 2. “reflscale >> 1” does the job perfectly and is a lot faster.

Precalculate

Precalculating most stuff was what gave the biggest improvements in cycle reduction. I’ve moved almost everything, apart from the sampling from the background, to the Init functions and made it accessible by array indices.

I started precalculating stuff when I noticed the “sin()” calls always used a number of 0 to 128 as arguments. I created an array of precalculated sines and referenced to that, giving a great boost in speed. I wanted to do the same for the distances, using an array of 64×64, because the distances are the same for all quadrants of the circle. This gave me an off-by-one error, making the code draw 2 unwanted lines. Since memory usage wasn’t the focus, I figured I could just use 128×128 arrays for the calculations, avoiding calls to “abs()”.

After this, I sat down with a classmate, talking about which optimizations we used and soon figured out that practically everything can be cached quite easily. The entire specular highlight can be saved in an array, getting rid of “sqrt()”-calls, “pow”-calls, “sin()”-calls, and floats in the rendering of each ball every frame. The highlight-array is basically just an overlay for the ball, blended with “AddBlend()”. All the heavy code is now in the Init-function, basically leaving only integer arithmetic, sampling from an image, blending, and bitshifting in the DrawBall-function. Pre-rendering every possible position for a ball could also be a solution, but having 800×600 pre-rendered balls in memory isn’t a neat solution in my opinion.

Avoid conditional jumps

Unrolling my loops would probably speed things up, but I read that the compiler unrolls the loops automatically. An old forum post a user states that the Visual C++ compiler unwinds loops where possible to increase performance. My project settings are set to produce the fastest code (opposed to the smaller code option).

Get out early

The “Get out early”-principle basically means to break the loop if the rest of the iterations aren’t helpful anymore. I tested code which broke the X-loop after it drew the last pixel of that row. Unfortunately, the checks for these last pixels increased the amount of cycles more than it saved, which is why I don’t break the loop.

Conclusion

The core of this optimization challenge was precalculation (caching) and getting rid of expensive function calls. I got the ball to render more than 10 times as fast and I can run the program drawing 100 balls on screen with over 30 FPS on my laptop. I’m happy with the result, yet it frustrates me a little bit that I can’t find anything else in that piece of code to optimize, but I guess I’ll learn more ways to do that in future lectures. Thanks for reading!

For an assignment for Programming 3 at IGAD, I have to optimize a piece of code. The code transforms, sorts, and renders an amount of sprites. Optimization of the rendering was done in class, so the sorting is the biggest bottleneck at the moment. Which is what I will dedicate this post to. I’ve found some sorting algorithms that I think are very interesting. The ones I will talk about are QuickSort, Radix Sort, and Tree Sort. The algorithm used in the code at first is an unoptimized Bubble Sort, which is very slow.

The sorting algorithm will have to deal with a high amount of sprites to sort, based on their Z-value, which is a floating-point number. The amount of sprites ranges is at least above 5000 and the assignment is to make the code render as many sprites on screen as I can.

Tree Sort

The first decent algorithm I imagined without research was a tree structure, where you would put all data in a binary tree. This automatically sorts the tree, which you could flatten back to an array quite easily. Apparently, this exists and isn’t a terrible solution for sorting. The only problem you face is when you have an unbalanced tree. If you have the maximum value as a first value, anything that gets added will get added to the left child nodes. With a bit of bad luck, this could be the case for a lot of elements, making you traverse every element before adding a new one.

The ease of implementation is what would make this an option for the simulation that I have to optimize. I will not use this one, but I will give example pseudo-code of how I would implement it. It can probably optimized in really simple ways, but since I’m not using this algorithm, I see no need in working on that at the moment. Adding to the tree would be as follows.

[code language=”cpp”]struct TreeNode
{
/*
* I’m using float3-vectors, this could be a Sprite as well.
* The code just draws sprites at positions.
*/
float3 value;
TreeNode* leftNode;
TreeNode* rightNode;

TreeNode(float3 a_value)
: value(a_value), leftNode(nullptr), rightNode(nullptr){}

~TreeNode()
{
if(leftNode) delete leftNode;
if(rightNode) delete rightNode;
}

void Insert(float3& a_other)
{
if(a_other.z <= value.z)
{
if(leftNode == nullptr)
leftNode = new TreeNode(a_other);
else
leftNode->Insert(a_other);
}
else
{
if(rightNode == nullptr)
rightNode = new TreeNode(a_other);
else
rightNode->Insert(a_other);
}
}

//float3 pointer to array, int pointer
void Flatten(float3* a_array, int& a_index)
{
if(leftNode != nullptr)
leftNode->Flatten(a_array, a_index);

a_array[a_index++] = value;

if(rightNode != nullptr)
rightNode->Flatten(a_array, a_index);
}
};

//Setting the first position vector as RootNode
TreeNode* root = new TreeNode(ListOfPositions[0]);

//DOTS is a define which is the number of sprites drawn
for(int i = 1; i < DOTS; i++)
{
root->Insert(ListOfPositions[i]);
}

//Now, to flatten the tree back to an array.
int index = 0;
root->Flatten(ListOfPositions, index);

//Don’t forget to clean up the tree!
delete root;[/code]
I tried this code in the application and quite quickly discovered that this is a slow method of sorting, compared to Quicksort. This might be because it is a completely unbalanced tree. The results vary, but it sometimes uses 100 times the amount of cycles that Quicksort uses.

Radix Sort

The first thing I did when I started this assignment was to look for sorting algorithms. There is an awesome visualization of 15 algorithms on YouTube. This video features the Radix Sort (LSD) and Radix Sort (MSD). I will focus on LSD (Least Significant Digit) here, because that is what I tried to implement.

The idea of Radix Sort is to sort numbers in several passes. Every pass sorts the list by a digit in the number. If you have an array with {105, 401, 828, 976}, you can sort on the last digit. {105, 401, 828, 976} would become {401, 105, 976, 828}. After this, you sort on the second digit, making {401, 105, 976, 828} into {401, 105, 828, 976}. The last digit makes {401, 105, 828, 976} into {105, 401, 828, 976}, and we’re done sorting. The beauty of this algorithm is that you can do it without comparing numbers to eachother. I will explain how in a while.

Another cool property of this algorithm is that it is a stable sorting algorithm. This means that if you have two objects in an array with the same comparing value (e.g. {Vector3(100, 20, 3), Vector3(526, -10, 3)} when comparing Z-values), they are guaranteed to appear in the same order in the array. The second element will never be inserted before the first element. This is quite useful, because two objects with the same Z-value and similar X and Y positions might end up Z-fighting, a problem I am facing with Quicksort at the moment.

For this algorithm, you don’t compare values to eachother. The idea is to use buckets to put the objects in. For the previous example, you can have 10 buckets. A bucket per digit (0..9). When you are done filling the buckets, you loop through the buckets, adding all the items in the bucket to an array, making it all sorted on the current radix. For the previous example, this required three passes, one pass per digit. This makes the complexity of Radix Sort O(n*k) where k is equal to the amount of passes. This is very fast, but not applicable to all sorting problems. The good thing is, I can use this to sort floating-point numbers.

Floating-point numbers are difficult to sort this way, since the radices aren’t obvious. What you can do, however, is convert the float to an unsigned integer and using the hexadecimal values to sort them. I will not go in to detail on how to do this, since there are amazing articles by Pierre Terdiman and Michael Herf on Radix Sorting (negative) floating-point numbers. The idea is that most compilers comply to the IEEE 754 standard for representation of floating-point numbers in memory, making the least significant bits in the memory representation also the least significant digits in the floating-point number.

Quicksort

Quicksort is the algorithm I ended up using, since I couldn’t get the Radix Sort to work properly and Quicksort is easier to implement. Quicksort has the advantage that the sorting is in-place, meaning you don’t need additional memory for the sorting process. A downside to Quicksort is that the algorithm isn’t stable, giving Z-fighting issues in this demo.

The concept of Quicksort is to select a pivot point in the array (any random number, the median would be ideal, but costs more time to compute) and put lower numbers to the left of this pivot and higher numbers to the right. When this is done, you partition the array into several smaller partitions to sort the smaller and higher blocks. This process is recursive and ends when the partition size is too small to swap things over the pivot (for example, just the pivot left in the partition would indicate that that partition is sorted, or at least doesn’t require sorting).

Conclusion

This concludes my post about sorting algorithms. The one I picked was Quicksort, since it is easy to understand, implement, and find reference for. It is incredibly fast, but I consider the Z-fighting issues annoying. I’d require a stable sorting algorithm to get rid of that. Radix Sort would be a viable candidate for that, but for the time I had, it took too much to fully comprehend and implement it. The Tree Sort is really easy to implement, since I made up the code as I wrote this post, but it’s slow as well. It could use some clever optimizing, but I wanted to focus on getting the program fast first. The downside to Radix Sort and Tree Sort is that it isn’t in-place, meaning that you need extra memory for sorting the arrays. Memory wasn’t an issue in this assignment, but it can be an issue in future projects, which is why I took it into consideration when picking Quicksort.