Reflective Shadow Maps (RSM) is an algorithm that extends “simple” Shadow Maps. The algorithm allows for a single diffuse light bounce. This means that, besides direct illumination, you get indirect illumination. This article breaks down the algorithm from the paper to explain it in a more human-friendly way. I will also briefly cover Shadow Mapping.
Shadow Mapping
Shadow Mapping (SM) is a shadow generation algorithm. This algorithm stores the distance from a light to an object in a depth map. Figure 1 shows an example of a depth map. It stores the distance (depth) per pixel. So, when you have a depth map from a light’s point of view, you then draw the scene from the camera’s point of view. To determine if an object is lit, you check the distance from the light to that object. If the distance to the object is greater than what is stored in the shadow (depth) map, the object is in the shadow. This means the object must not be lit. Figure 2 shows an example. You do these checks per pixel.

Figure 1: This image shows a depth map. The closer the pixel is, the brighter it appears. |
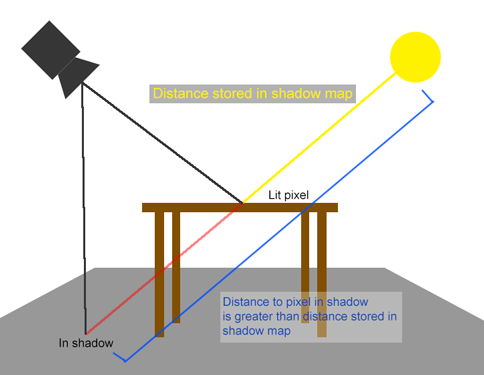
Figure 2: The distance from the light to the pixel in the shadow is greater than the distance stored in the depth map. |
Reflective Shadow Mapping
Now that you understand the basic concept of Shadow Mapping, we continue with Reflective Shadow Mapping (RSM). This algorithm extends the functionality of “simple” Shadow Maps. Besides depth data, you also store world space coordinates,the world space normals, and the flux. I will explain why you store these pieces of data.
The data
World space coordinates
You store the world space coordinates in a Reflective Shadow Map to determine the world space distance between pixels. This is useful for calculating light attenuation. Light attenuates (becomes less concentrated) based on the distance it travels. The distance between two points in space are used to calculate how intense the lighting is.
Normals
The (world space) normal is used to calculate the light bouncing off of a surface. In case of the RSM, it is also used to determine the validity of the pixel as a light for another pixel. If two normals are very similar, they will not contribute much bouncing light for each other.
(Luminous) Flux
Flux is the luminous intensity of a light source. The unit of measurement for this is Lumen, a term you see on light bulb packages nowadays. The algorithm stores the flux for every pixel checked while drawing the shadow map. Flux is calculated by multiplying the reflected light intensity by a reflection coefficient. For directional lights, this would give a uniformly lit image. For spot lights, you take the angle falloff into consideration. Attenuation and receiver cosine are left out of this calculation, because this is taken into account when you calculate the indirect lighting. The article does not go into detail about this. Figure 3 shows an image from the RSM paper displaying the flux for a spot light in the fourth image.

Figure 3: This image shows the four maps contained in an RSM. From left to right; depth map, world space coordinates, world space normals, flux
Applying the data
Now that we have generated the data (theoretically), it is time to apply it to a final image. When you draw the final image, you test all lights for every pixel. Besides just lighting the pixels using the lights, you now also use the Reflective Shadow Map.
A naive approach to calculating the light contribution is to test all texels in the RSM. You check if the normal of the texel in the RSM is not pointing away from the pixel you are evaluating. This is done using the world space coordinates and the world space normals. You calculate the direction from the RSM texel’s world space coordinates to that of the pixel. You then compare that to the direction the normal is pointing to, using the vector dot product. Any positive value means the pixel should be lit by the flux stored in the RSM. Figure 4 demonstrates this algorithm.
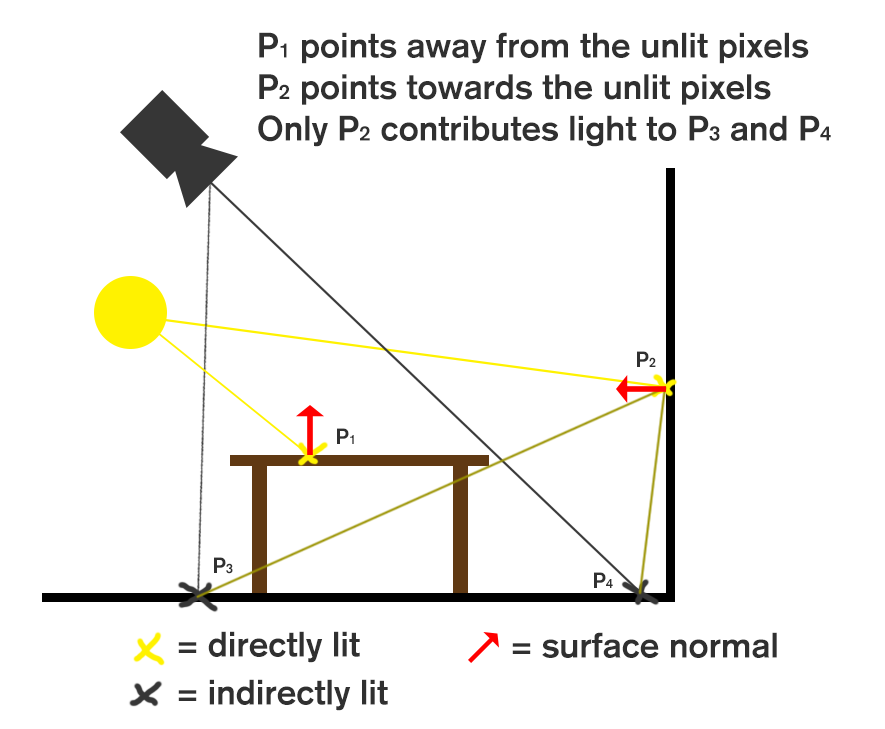
Figure 4: Demonstration of indirect light contribution based on world space positions and normals
Shadow maps (and RSMs) are large by nature (512×512=262144 pixels), so doing a test for every texel is far from optimal. Instead, it is best to take a set amount of samples from the map. The amount of samples you take depends on how powerful your hardware is. An insufficient amount of samples might give artifacts like banding or flickering colors.
The texels that will contribute most to the lighting result are the ones closest to the pixel you are evaluating. A sampling pattern that takes the most samples near the pixel’s coordinates will give the best results. The paper describes that the sampling density decreases with the squared distance from the pixel we are testing. They achieve this by converting the texture coordinates to polar coordinates relative to the point we are testing.
Since we are doing “importance sampling” here, we need to scale the intensity of the samples by a factor related to the distance. This is because samples that are further away get sampled less often, but would in reality still contribute the same amount of flux. Samples closer by get sampled more often, but samples farther away are more intense. This evens out an inequality while keeping the sample count low. Figure 5 shows how this works.
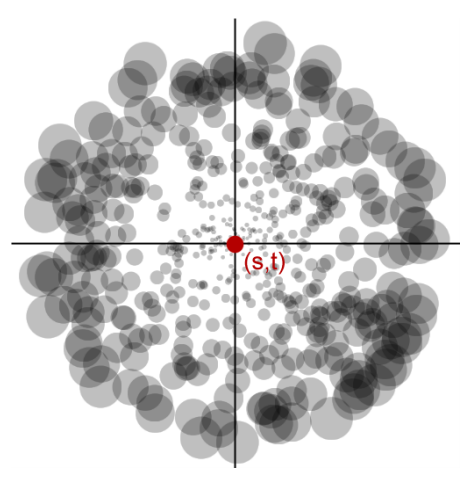
Figure 5: Importance sampling. More samples are taken from the center and samples are scaled by a factor related to their distance from the center point. Borrowed from the RSM paper.
When you have a sample, you treat that sample the same as you would treat a point light. You use the flux value as the light’s color and only light objects in front of this sample.
The paper goes into more detail on how to further optimize this algorithm, but I will stop here. The section on Screen-Space Interpolation describes how you can gain more speed, but for now I think importance sampling will suffice. I am glad to say that I understand the RSM algorithm enough to build an implementation in C++/DirectX11. I will do my best to answer any questions you may have.
